Research Projects

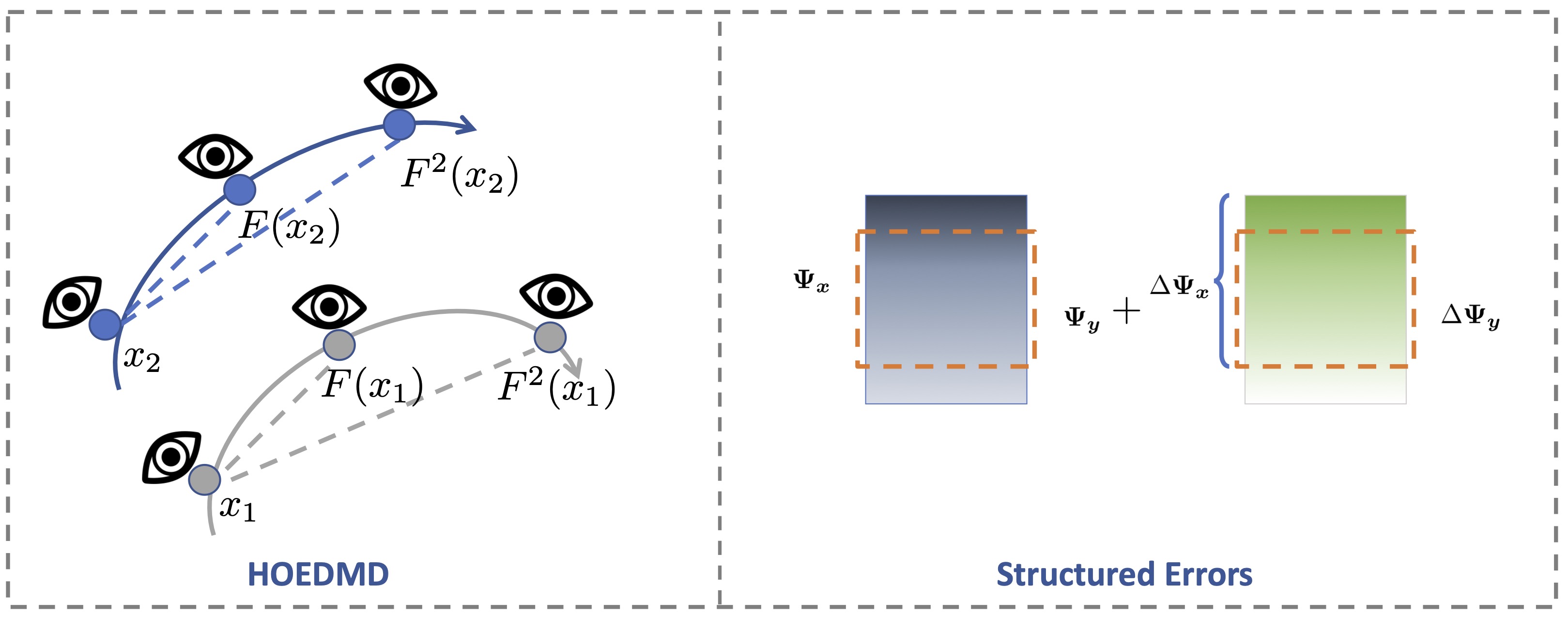
Higher Order Extended Dynamic Mode Decomposition Theory and Applications

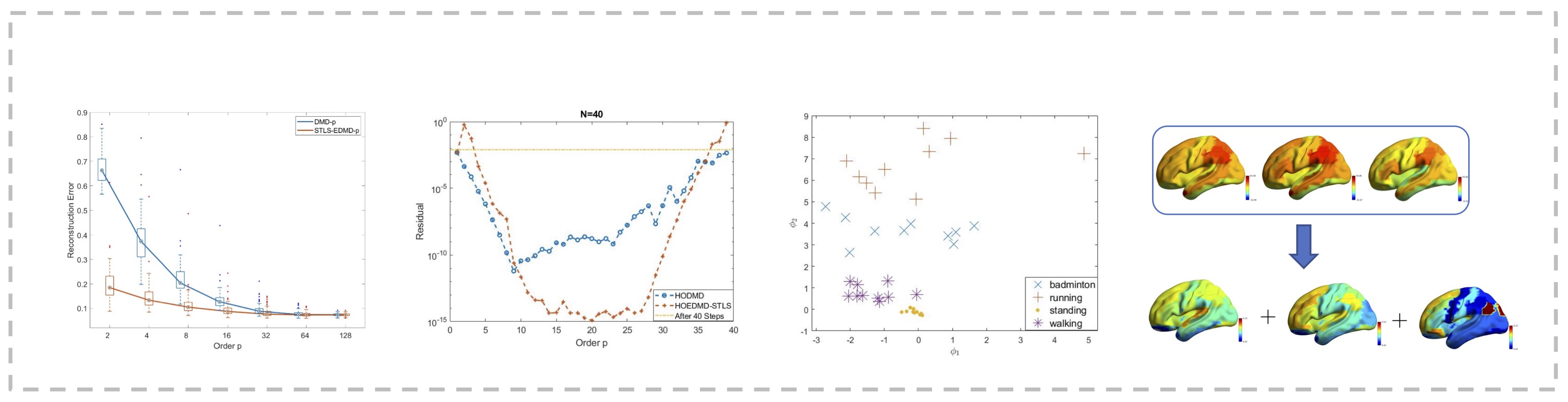
• Developed the higher order extended dynamic mode decomposition (HOEDMD) method for analyzing dynamics from snapshots. Introduced the structured total least squares (STLS) technique for denoising and debiasing and kernel methods for nonlinearity within the HOEDMD framework.

• Implemented efficient numerical algorithms to enhance the algorithm’s performance and scalability.
• Provided insights with application in multi-linear PageRank acceleration, time series parametrization and fMRI signal analysis.

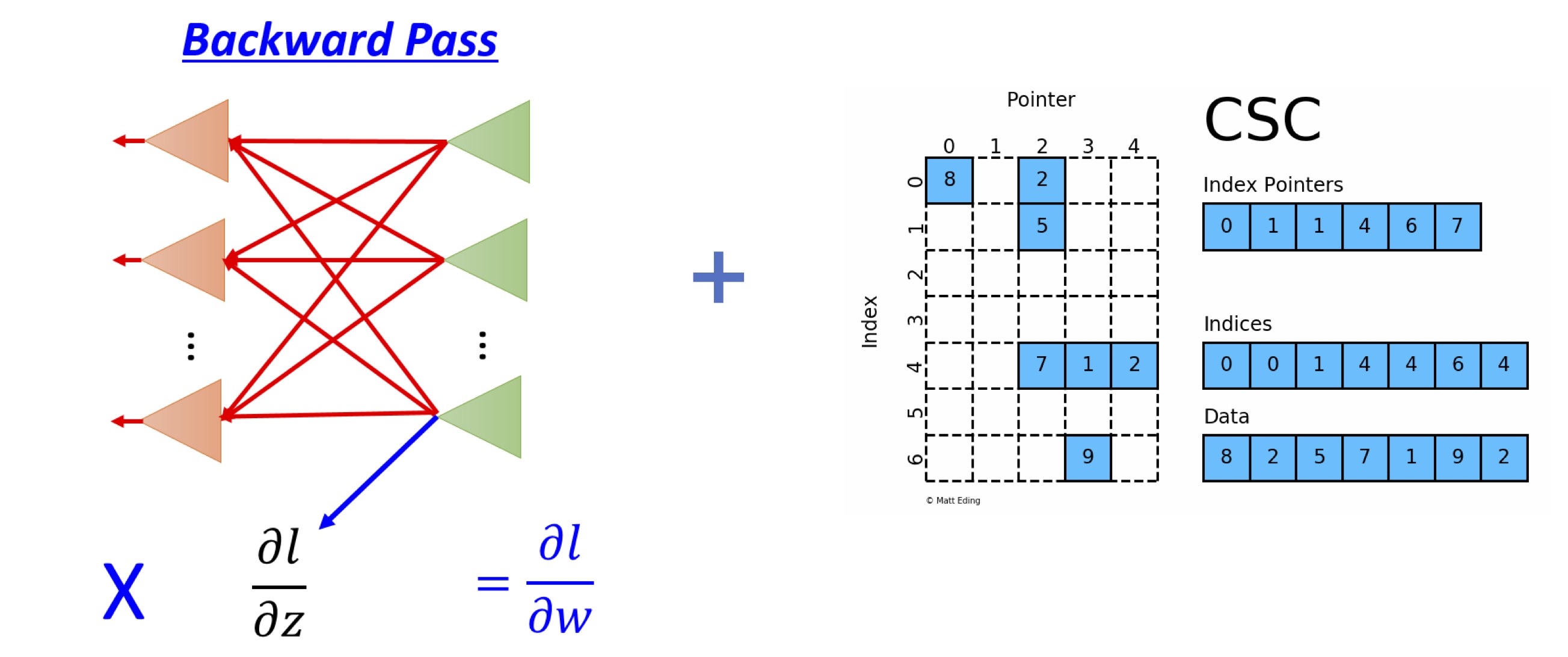
Differentiating Sparse Matrix Operations with Reversible Programming

• Developed SparseADRules.jl to handle automatic differentiation for sparse matrix operations in Julia.
• Ported the generated backward rules, implemented robust unit tests and automated CI pipelines.
• Tested SparseADRules.jl with a 1k*1k sparse matrix, achieving a 20x speedup in computation and 50% memory savings.

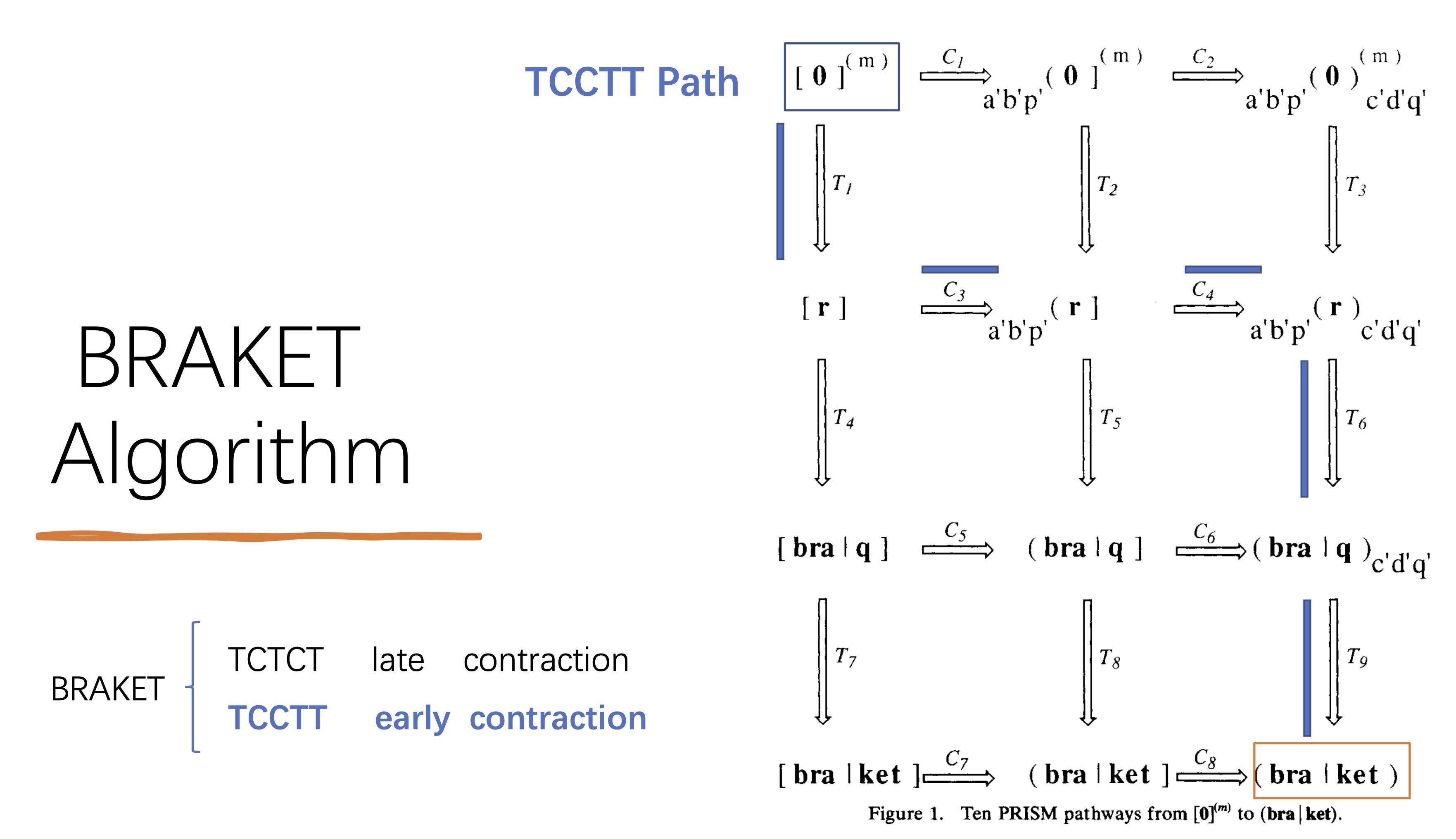
Acceleration of Electron Repulsion Intergrals Computation

• Contributed to the development of the BRAKET algorithm, efficient in terms of both FLOPS and memory savings when compared to the Head-Gordon and Pople algorithm.
• Implemented the algorithm using CUDA for accelerated integral computation, achieving a tenfold speedup in computation time compared to the PySCF package.